Zahra Ediana
XI IPS 3
A.barisan dan deret aritmetika
barisan dan deret aritmetika atau dikenal sebagai barisan dan deret hitung adalah barisan yang mempunyai pola tertentu, yakni selisih dua suku berturutan sama dan tetap. Dengan kata lain, setiap suku (kecuali suku pertama) pada barisan aritmetika diperoleh dari suku sebelumnya dengan menambah bilangan tetap (3,5,7,9,11,13)
- Rumus untuk menentukan suku ke-n dari barisan aritmetika:
- Rumus untuk mencari beda pada barisan aritmetika:
- Contoh Barisan Aritmetika:
- CONTOH:
1.) Diketahui sebuah barisan aritmetika 15, 19, 23, 27, 31, … .
a. Tentukan suku ke 25!
b. Tentukan 10 suku pertama!
Pembahasan:
2.) suatu bentuk deret aritmetika adalah 5, 15, 25, 35, …. Berapakah jumlah 10 suku pertama dari deret aritmetika tersebut?
Diketahui:
n = 10
U1 = a = 5
b = 15 – 5 = 25 – 15 = 10
Jawaban:
Sn = (2a + (n-1) b )
S10 = ( 2. 5 + (10 -1) 10)
= 5 ( 10 + 9.10)
= 5 x 100 = 500
Jadi, jumlah S10 dalam deret aritmetika tersebut, yakni 500.
3.) Seoang pegawai kecil menerima gaji tahun pertama sebesar Rp3.000.000,00. Setiap tahun gaji tersebut naik Rp500.000,00. Jumlah uang yang diterima pegawai tersebut selama sepuluh tahun adalah …
Diketahui:
Gaji pertama = a = Rp3.000.000,00
Kenaikan gaji tiap tahun = b = Rp.500.000
Gaji tahun kesepuluh = U10
Jumlah gaji selama sepuluh tahun = S10
Jawaban:
Un = a + (n – 1)b
U10 = 3.000.000 + (10 – 1)500.000
= 3.000.000 + (9 × 500.000)
= 3.000.000 + 4.500.000
= 7.500.000
Jadi, gaji pegawai yang didapatkan pada tahun kesepuluh adalah sebesar Rp 7.500.000,00
- https://akupintar.id/info-pintar/-/blogs/barisan-deret-aritmetika-dan-geometri-pengertian-rumus-dan-contoh-soal
- https://www.gramedia.com/literasi/barisan-aritmetika/
- Rumus untuk mencari rasio pada barisan geometri:
3, 12, 48, 192, …
a. Tentukan suku ke-10 dari barisan geometri tersebut!
b. Tentukan jumlah 5 suku pertama dari barisan geometri tersebut!
Pembahasan:
2.) di ketahui rumus deret geometri 3 + 6 + 12 + 24 + .. dari deret tersebut, berapakah jumlah enam suku pertama nya
jawab:
Dari deret geometri di atas, diketahui a = 2, dan r = 2 yang diperoleh dari;
Sehingga, nilai suku ke-13 bisa dihitung dengan cara:
Un = arn-1
U13 = 3 x 213-1 = 3 x 212 = 12.288
- https://katadata.co.id/intan/berita/62d95448a6b5e/mempelajari-rumus-deret-geometri-lengkap-dengan-contoh-soalnya
- https://akupintar.id/info-pintar/-/blogs/barisan-deret-aritmetika-dan-geometri-pengertian-rumus-dan-contoh-soal
Bunga yaitu selisih antara jumlah uang yang dipinjamkan oleh pemodal dengan jumlah uang yang akan dikembalikan oleh pemakai modal menurut kesepakatan bersama.
Adapun besarnya bunga dipengaruhi oleh: besarnya jumlah uang yang dipinjam, jangka waktu untuk meminjam, dan tingkat suku bunga / persentase. Bunga dibedakan menjadi 2 jenis, yakni bunga Tunggal dan bunga Majemuk.
- Bunga tunggal
Bunga tunggal yaitu bunga yang dibayar untuk setiap periodenya dengan jumlah yang tetap. Bunga tunggal ini dihitung menurut modal awal.
- Rumus bunga tunggal pada akhir periode:
- Rumus besarnya modal pada akhir;
Keterangan:
B = bunga
M0 = modal awal
Mt = modal pada akhir periode – t
t = periode
r = tingkat suku bunga (persentase)
- Bungan majemuk
Bunga majemuk yaitu, bunga yang dihitung menurut jumlah modal yang dipakai ditambahkan dengan akumulasi bunga yang telah terjadi. bunga majemuk ini sering disebut dengan bunga berbunga, bunga majemuk dapat dihitung dengan menggunakan deret geometri.
Misalkan, Modal Sejumlah M0, akan diberlakukan bunga majemuk,dengan tingkat suku bunga i (dalam persentase) per periode waktu. Besarnya modal saat periode ke-t (Mt) bisa dihitung dengan cara:
Sehingga, rumus untuk besar modal pada periode ke-t dengan bunga majemuk yaitu;
keterangan;
Mt = modal pada akhir periode – t
M0 = modal awal
i = tingkat suku bunga
t = periode
- Pertumbuhan yaitu pertambahan atau kenaikan nilai suatu besaran terhadap besaran yang sebelumnya yang umumnya mengikuti pola aritmatika (linier) atau geometri (eksponensial).
Contoh dari pertumbuhan misalnya perkembangbiakan amoeba dan pertumbuhan penduduk.
- Rumus pertumbuhan linear;
- Sedangkan rumus pertumbuhan eksponensial;
Keterangan;
Pn = nilai besaran setelah n periode
P0 = nilai besaran pada awal periode
b = tingkat pertumbuhan
n = banyaknya periode pertumbuhan
- Contoh soal:
Banyak penduduk kota A setiap tahun meningkat 2% secara eksponensial dari tahun sebelumnya. Tahun 2013 penduduk di kota A sebanyak 150.000 orang. Hitung banyak penduduk pada tahun 2014 dan 2023!
Jawab:
![]()
Banyak penduduk pada tahun 2014 (artinya 1 tahun setelah 2013, maka n = 1):

Banyak penduduk pada tahun 2023 (n=2023-2013=10):

- Peluruhan
Peluruhan ( penyusutan) yaitu berkurangnya nilai atau penurunan suatu besaran terhadap nilai besaran yang sebelumnya, yang umumnya mengikuti pola aritmatika (linier) atau geometri (eksponensial). Peluruhan misalnya, peluruhan zat radioaktif dan penurunan harga jual mobil.
- Rumus peluruhan linear;
- Rumus peluruhan eksponensial;
Keterangan;
Pn = nilai besaran setelah n periode
P0 = nilai besaran pada awal periode
b = tingkat peluruhan
n = banyaknya periode pertumbuhan
- Contoh soal:
Suatu bahan radioaktif yang semula berukuran 125 gram mengalami reaksi kimia sehingga menyusut 12% dari ukuran sebelumnya setiap 12 jam secara eksponensial. Tentukan ukuran bahan radioaktif tersebut setelah 3 hari!
Jawab:
![]()
Peluruhan terjadi setiap 12 jam, sehari peluruhan terjadi 2 kali, 3 hari = 72 jam terjadi 6 kali peluruhan.
![]()

- https://rumushitung.com/2021/04/16/bunga-pertumbuhan-peluruhan-pengertian-jenis-dan-rumusnya/
- https://www.ruangguru.com/blog/pertumbuhan-dan-peluruhan-matematika
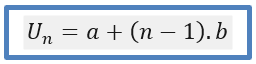








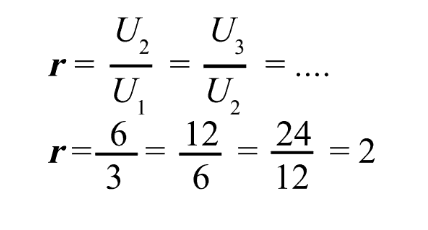


Komentar
Posting Komentar