Zahra Ediana
X IPS 1
PERBANDINGAN TRIGONOMETRI PADA SEGITIGA SIKU-SIKU
Trigonometri sangat erat kaitannya dengan sudut segitiga, karena asal kata trigonometri sendiri yang berarti mengukur tiga sudut (berasal dari kata Yunani, trigonon: tiga sudut dan metro: mengukur). Jika berbicara mengenai trigonometri tidak akan bisa lepas dari sinus, cosinus, tangen, cosecan, secan, dan cotangen.
Perbandingan Trigonometri dari Suatu Sudut pad aSegitiga Siku-Siku
dengan a dan b adalah sisi siku-siku dan c adalah sisi miringnya. Untuk lebih jelasnya maka perhatikan gambar berikut.

Perbandingan Sinus (sin), Cosinus (cos), Tangen (tan), Cosecan (scs), Secan (sec), dan Cotangen (cot).

Sisi Miring adalah sisi di depan sudut siku-siku.
Sisi Depan adalah sisi di depan sudut α.
Sisi Samping adalah sisi siku-siku lainnya.
Setelah mengetahui sisi miring, sisi depan, dan sisi samping, selanjutnya kita akan membahas definisi sinus, cosinus, tangen, cosecan, secan, dan cotangen.

Contoh:
Tentukan nilai sinus, cosinus, dan tangen untuk sudut Q dan R pada segitaga berikut.

Jawab:






Nilai Perbandingan Trigonometri Sudut Istimewa
Untuk mencari sudut istimewa dapat digunakan beberapa bidang datar untuk mencara nilai sudut istimewa tersebut.
Untuk mencari nilai perbandingan sudut  kita menggunakan segitiga sama sisi.
kita menggunakan segitiga sama sisi.

Segitiga sama sisi memiliki sisi-sisi yang sama panjang dan sudut yang sama besar. Sudut-sudut segitiga sama sisi masing-masing adalah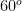 .
.
Segitiga sama sisi ABC memiliki panjang sisi-sisinya adalah 2x satuan. Titik D adalah titik tengah AB, sehingga jika ditarik garis dari titik C ke titik D akan membagi segitiga sama sisi tersebut menjadi segitiga sama sisi, dengan sudut siku-siku di D.
Karena titik D merupakan titik tengah, maka panjang AD =BD = Sudut 30 dan 60

Segitiga sama sisi memiliki sisi-sisi yang sama panjang dan sudut yang sama besar. Sudut-sudut segitiga sama sisi masing-masing adalah
Segitiga sama sisi ABC memiliki panjang sisi-sisinya adalah 2x satuan. Titik D adalah titik tengah AB, sehingga jika ditarik garis dari titik C ke titik D akan membagi segitiga sama sisi tersebut menjadi segitiga sama sisi, dengan sudut siku-siku di D.
maka diperoleh:
Sehingga
1. Untuk
2. Untuk
Sudut 45
 Pada persegi di atas, jika dibuat garis diagonal dari titik A ke titik C akan membentuk segitiga siku-siku yang memiliki dua sisi yang sama.
Pada persegi di atas, jika dibuat garis diagonal dari titik A ke titik C akan membentuk segitiga siku-siku yang memiliki dua sisi yang sama.Perhatikan segitiga ABC.
Tabel 1 Nilai perbandingan trigonometri untuk sudut-sudut istimewa
Contoh:
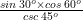

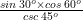



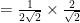
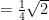


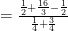
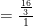
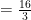
Untuk mengetahui perbandingan trigonometri sudut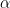 didefinisikan sebagai berikut:
didefinisikan sebagai berikut:



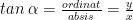
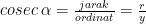


Sudut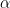 di kuadran I, jika
di kuadran I, jika 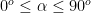
Sudut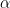 di kuadran II, jika
di kuadran II, jika 
Sudut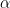 di kuadran III, jika
di kuadran III, jika 
Sudut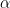 di kuadran IV, jika
di kuadran IV, jika 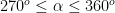
Tanda nilai perbandingan trigonometri sudut-sudut di berbagai kuadran sebagai berikut.
Contoh:
Diketahui titik P(-5, 12). Jika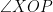 , maka tentukan sin
, maka tentukan sin 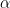 , cos
, cos 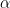 , dan tan
, dan tan 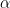
.Jawab:

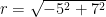
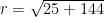

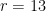
| 0 | 1 | ||||
| 1 | 0 | ||||
| 0 | 1 | – | |||
| – | 2 | 1 | |||
| 1 | 2 | – | |||
| – | 1 | 0 |
Contoh:
Hitunglah:
Jawab:
Perbandingan Trigonometri Sudut-Sudut di Berbagai Kuadran
Untuk mengetahui perbandingan trigonometri sudut

Sudut
Sudut
Sudut
Sudut
Tanda nilai perbandingan trigonometri sudut-sudut di berbagai kuadran sebagai berikut.
| Perbandingan Trigonometri | Sudut di Kuadran | |||
| I | II | III | IV | |
| + | + | – | – | |
| + | – | – | + | |
| + | – | + | – | |
| + | + | – | – | |
| + | – | – | + | |
| + | – | + | – | |
Contoh:
Diketahui titik P(-5, 12). Jika
.Jawab:
Komentar
Posting Komentar